Chapter-10
Light Reflection and Refraction
• Light is the form of energy that enables us to see.
Properties of Light
| • Electromagnetic wave, so does not require any medium to travel. |
| • Light tends to travel in straight line. |
| • Light has dual nature i.e., wave as well as particle. |
| • Light casts shadow. |
| • Speed of light is maximum in vaccum. Its value in 3 x 108 ms -1. |
| • When light falls on a surface, following may happen : |
| (a) Reflection (b) Refraction (c) Absorption |
REFLECTION
Bouncing back of light when it strike on a polished surface like mirror.
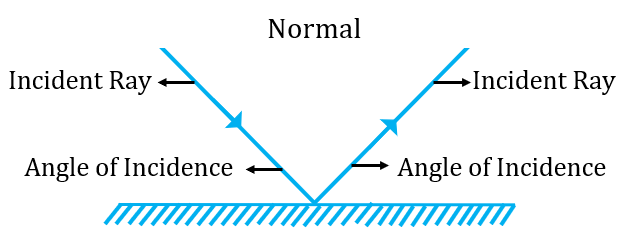
Laws of Reflection :
| (1) Angle of incidence is equal to the angle of reflection. |
| (2) The incident ray, the reflected ray and the normal at the point of incidence, all the lie in the same place. |
Image : It is point where atleast two light rays actually meet or appear to meet.
| Real Image | Virtual Image |
|---|---|
| • Formed when light rays actually meet. | • Formed when light rasys appear to meet. |
| • Can be obtained on screen. | • Can't be obtained on screen |
| • Inverted. | • Erect. |
| • E.g., image formed on cinema screen. | • E.g., image formed by place mirror or convex mirror. |
Image Formed by Place Mirror
Characteristics of Image
| (i) Virtual and ercet. |
| (ii) Size of image is equal to the size of object. |
| (iii) Image is formed as far behind the mirror as the object is in fromt of it. |
| (iv) Laterally inverted. |
Lateral Inversion : The right side of the object appears left side of the image and vice-versa.
Application of Lateral Inversion : The word AMBULANCE is written as AMBULANCE so that it can be read correctly in rear view mirror of vehicles going in front of it.
Spherical Mirrors : Mirrors whose reflecting surface is curved.
| Convex Mirror | Concave Mirror |
|---|---|
| • Reflecting surface is curved outwards. | • Reflecting surface is curved inwards |
| • Diverging mirror | • Converging mirror |
| • Principal axis : The line joining the pole and center of curvature. |
| • Pole (P) : The center of the spherical mirror. |
| • Aperture (MN) : It is the effective diameter of of the spherical mirror. |
| • Center of Curvature (C) : The centre of the hollow glass sphere of which the mirror was a part. |
| • Radius of Curvature (R) : The distance between the pole and the centre of curvature. |
| • • Focus (F) : The point on principal axis where all the parallel light rays actually meet or appear to meet after reflection. |
| • • Focal Length (f) : The distance between the pole and the focus |
Relationship between focal length and radius of curva true :
R
f = ---
2
Rules for making ray diagrams by concave mirror
(i) A ray parallel to the principal axis will pass through the principal focus, after reflection.
(ii) A ray passing through the principal focus of concave mirror will emerge parallel to principal axis after reflection.
(iii) A ray of light passing through the centre of curvature of a concave mirror is reflected back along the same path as it is a normally incident ray.
(iv) A ray incident obliquely to the principal axis of a concave mirror is reflected obliquely making equal angle.
Ray diagrams for images formed by concave mirror
| (i) When object is at infinity : | Image |
| Position - At 'F' Nature - Real, inverted Size - Point sized or highly diminished |
|
| (ii) When object is beyond 'C' | Image |
| Position - Between 'F' and 'C' Nature - Real, inverted Size - Diminished |
|
| (iii) When object is at 'C' | Image |
| Position - At 'C' Nature - Real, inverted Size - Same size as that of object |
|
| (iv) When object is placed between 'F' and 'C' | Image |
| Position - Beyond 'C' Nature - Real, inverted Size - Enlarged |
|
| (v) When object is placed at 'F' | Image |
| Position - At Infinity Nature - Real, inverted Size - Highly enlarged |
|
| (vi) When object is between | Image |
| Position - Behind the mirror Nature - Virtual, ercet Size - Enlarged |
Uses of Concave Mirror
(i) Used in torches, search lights and vehicles headlights to get powerful parallel beam of light.
(ii) Concave mirrors are used by dentists to see large image of teeth of patients. (Teeth have to be placed between pole and focus
(iii) Concave mirror is used as shaving mirror to see a larger image of the face.
(iv) Large concave mirrors are used to concentrate sunlight to produce heat in solar furnace.
Rules for image formation by Convex Mirror
(i) A ray of light parallel to the principal axis of a convex mirror appear to diverge from the principal focus.
(ii) A ray which is directed towards the focus of the convex mirror will emerge parallel to the principal axis after reflection.
(iii) A ray directed towards to center of a convex mirror is reflected back along the same.
(iv) A ray incident obliquely to the principal axis is reflected obliquely.
Ray diagrams of images formed by Convex Mirror
| (i) When object is placed at infinity : | Image |
| Position - At 'F' Nature Virtual, erect Size Point sized |
|
| (ii) When object is placed between pole and infinity : | Image |
| Position - Between 'P' and 'F' Nature Virtual, ercet Size Diminished |
• A full length image of a tall building/ tree can be seen in a small convex mirror.
Uses of Convex Mirror
(i) Convex mirrors are used as rear view mirrors in vehicles because
-
(a) they always give an erect through diminished image.
(b) they have a wider field of view as they are curved outwards.
(ii) Convex mirrors are used at blind turns and on points of merging traffic to facilitate vision of both side traffic.
(iii) Used in shops as security mirror.
Sign Convention for Reflection by Spherical Mirror
Or
New Cartesian Sign Convention
(i) The object is placed to the left of the mirror.
(ii) All distance parallel to the principal axis are measured from the pole of the mirror.
(iii) All distances measured in the direction of incident ray (along + X-axis) are taken as positive and those measured against the direction of incident ray (along - X-axis) are taken as negative.
(iv) Distance measured perpendicular to and above the principal axis are taken as positive.
(v) Distance measured perpendicular to and below the principal axis are taken as negative.
• Object distance = 'u' is always Negative.
• Focal length of concave mirror = Negative
• Focal length of convex mirror = Positive
Mirror Formula :
| Where, |
v = Image distance u = Object distance f = Focal lenght |
Magnification of Spherical Mirrors
| m = Height of image Height of object |
|
| m = hi ho |
|
| Also, | |
| m = - v u |
If 'm' is negative, image is real.
If 'm' is positive, image is virtual.
If hi = ho then m = 1, i.e., image is equal to object.
If hi < ho then m < 1 i.e., image is enlarged.
If hi > ho then m > 1 i.e., image is diminished.
| • Magnification of plane mirror is always + 1. '+' sign indicates virtual image. '1' indicates that images is equal to object's size. |
| • If 'm' is '+ve' and less than 1, it is a convex mirror. |
| • If 'm' is '+ve' and more than 1, it is a concave mirror. |
| • If 'm' is '.ve', it is a concave mirror. |
REFLECTION
Bending of light when it enters obliquely from one transparent medium another.
• Speed of light is maximum is vaccum. It is 3 x 108 m/s.
• Cause of refraction : Change in speed of light.
• Some examples of refraction :
(i) The bottom of swimming pool appears higher.
(ii) A pencil partially immeresed in water appears to be bent at the interface of water and air.
(iii) Lemons placed in a glass tumbler appear bigger.
(iv) Letters of a book appear to be raised when seen through a glass slab.
Refraction through glass slab
| • The extent of bending of ray of light at the opposite parallel faces of rectangular glass slab is equal and opposite, so the ray emerges parallel to incident ray. |
| • Lateral displacement depneds on : (a) Refractive index of glass slab. (b) Thickness of the glass slab. |
Laws of Refraction
(i) The incident ray, the refracted ray and the normal to the interface of two transparent media at the point of incidence, all lie in the same plane.
(ii) Snell's law : The ratio of sine of angle of incidence to the sine of angle of refraction is a constant, for a light of given colour and for a given pair of media.
Refractive index (n) : The ratio of speed of light in a given pair of media n=
n21 means refractive index of second medium with respect to first medium, and
n12 means refractive index of first medium with respect to second medium.
• Absolute Refractive Index : Refractive index of a medium with respect to vaccum or air.
• Refractive index of one medium is reciprocal of other's refractive index in a given pair.
If refractive index of medium 1 w.r.t. air is given as 1nair, and
If refractive index of medium 2 w.r.t. air is given as 2nair
Then, refractive index of medium 1 w.r.t. medium
• Refractive index of diamond is the heighest till date. It is 2.42. It means speed of light is times less in diamond than in vaccum.
• Optically denser medium : Out of two given media, the medium with higher value of rafractive index.
• Optically rarer medium : Out of two given media, the medium with lower value of refractive index.
• When light enters obliquely from a rarer to a denser medium, it bends towards the normal.
• When light enters obliquely from denser to a rarer medium, it bends away from the normal.
• Refractive index of a medium does not depend on physical density.
Spherical lens : A transparent medium bound by two surfaces, of which one or both surfaces are curved.
| Convex lens | Concave lens |
|---|---|
| • Thin from corners | • Thick from corners |
| • Thick at center | • Thin at centre |
| • Converging | • Diverging |
Rules for image formation by convex lens
(i) A ray light parallel to principal axis of a convex lens always pass through the focus on the other side of the lens.
(ii) A ray of light passing through the principal focus will emerge parallel to principal axis after refraction.
(iii) A ray of light passing through the optical center will emerge without any deviation.
Ray Diagrams of Imaged formed by Convex Lens
| (i) When object is at infinity : | Image |
| Position - At 'F2' Nature - Real, inverted Size - Point sized or heighly diminished |
|
| (ii) When object is beyond '2F1' | Image |
|
Position - Between 'F2' and '2F2' Nature - Real, inverted Size - Diminished |
|
| (iii) When Object is at '2F1' | Image |
| Position - At '2F2' Nature - Real, inverted Size - Same size |
|
| (iv) When object is between 'F1' and '2F1' | Image |
| Position - Beyond '2F2' Nature - Real, inverted Size - Enlarged |
|
| (v) When object is at 'F1' | Image |
| Position - At Infinity Nature - Real, inverted Size - Highly enlarged |
|
| (vi) When object is between 'F1' and optical centre | Image |
| Position - On the same side of the lens as object Nature - Virtual and erect Size - Enlarged On the basis of this position, this lens is also known as magnifying lens. |
Rules for Image Formation by Concave Lens
| S.No. | Light ray from object is | Ray diagram | How it appears after refraction |
|---|---|---|---|
| 1. | Parallel to the principal axis | After refraction from a conacve lens, the ray appears to diverge from the principal focus located on the same side of the lens | |
| 2. | Passing through a principal focus | After refraction from a concave lens, the ray appears to diverge from the principal focus located on the same side fo the lens | |
| 3. | Passing through the optical center of a lens | After refraction from a concave lens will emerge wihout any deviation |
Ray Diagrams of Images Formed by a Concave Lens
| (i) When object is placed at infinity : | Image |
|
Position - At 'F1' Nature - Virtual, erect Size - Point or highly diminished |
| (ii) When object is placed between infinity and optical centre | Image |
|
Position - Between 'F' and 'O' Nature - Virtual, erect Size - Diminished |
Sign Convention for Spherical Lenses
• Sing converntions are similar to the one used for spherical mirrors, except that measurements are taken from optical center of the lens.
• Focal length of convex lens = Positive
• Focal length of convex lens = Negative
Lens Formula :
Magnification :
| m = hi ho |
hi = height of image ho = height of object |
|
| Also, | ||
| m = v/u |
Power of a lens :
It is defined as the reciproca of focal length in meter.
The degree of convergence or divergence of light rays is expressed in terms of power.
1 1
power = __________________________ p = __
focal length (in meter) f
| •
SI unit of Power = dioptre = D 1 D = 1 m1 1 dioptre is the power of lens whose focal length is one meter |
| • Power of convex lens = Positive |
| • Power of concave lens = Negative |
•
1
power ____________________________
focal length or thickness
|
| • Power of a lens combination P = P1 + P2 + P3.............. |
